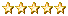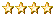Pikobrain has a random number generator (RNG). I thought it was creating actual random numbers, but it wasn't.
I noticed this when I made a program, that would go line by line on the screen. If the random number was divisible by <x>, a red pixel would be drawn. However, the image that program made was patterned. Like this:

This meant the RNG got into loops of numbers, such that these patterns would occur.
So, I sat down all evening, tinkering with various combinations of arithmetic and bitwise operations, with no success.
At least until by about 11pm, when it suddenly drew something like this:

As far as I am/was able to tell, that image has no patterns. The code that was creating this was also just the same kind of type I had tinkered around with all evening, but it just worked. It was also really simple, I'll show it soon.
Since then I have also made programs to test the nature of the new RNG.
The RNG does create patterns sometimes, but most of the time the image seems quite random.
I've printed random values, and I have been unable to find patterns when printing 512 random numbers in a row.
I also made a program that created two random numbers, and then checked how many random numbers later until those two random numbers appeared again. That doesn't really mean a pattern is found, since it could also be just by random. But it almost always took several thousand random numbers until the same two would appear again.
This is to say that the RNG is effective enough.
So, this is the code for it:
Code: Select all
random:
;random number generator
push cx ;store for assembly macros
push dx
mov ah, 0h ;get tick
int 1ah
mov ax, RANDOM_BUFFER
mov fs, ax
xor si, si
mov ax, [fs:si]
sub ah, dl ;update number = generate
sub al, ah ;al is random number returned
rol ax, 1h
mov [fs:si], ax ;store
pop dx
pop cx
retSo then I made something that is similar to what I have now, that would:
Code: Select all
sub ah, dl
sub al, ahEventually I removed some lines of code that dealt with if al==0 and used the rol ax, 1h : and it worked.
That's not well explained, but. I'll explain the new RNG:
It calls a BIOS function that returns the current tick. I use the byte in dl, that is increased ~18.2 times a second.
(By using that number I essentially get a "random" number when making the first random number)
I then subtract that from ah, which is subtracted from al (which is the random number "returned").
Then somehow, rotating ax by one step does magic, that causes the whole thing to be quite "random".
RANDOM_BUFFER (using fs:si) is simply were the random number will be stored, such that it can be updated the next time the RNG is called.
---
Many of the RNGs I looked at yesterday requires a lot of calculations. I tried using the classic "Linear Congruential" method, which is simple, but I found no good combination of numbers for 16-bit assembly.
So, I would call the method I ended up with yesterday small and effective in providing random bytes. It also seems as if ah is "random", so ax as a whole can be used as a random number.