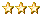Whatever your rotation code does, it does not adjust/compute the new weights appropriately. Most likely it just assumes that the weight of node 3 = +1: after an insert that assumption holds or you wouldn't trigger a right-right rotation, unfortunately, it doesnt necessarily hold after an delete. (Excercise for the reader to find out why)
Code: Select all
1 (+2)
/ \
a 3 (0)
/ \
2 4
/ \ / \
b c
next you rotate over 1-3-4, which is ok (1-3-2 would work as well, but here you can choose)
we know that
h(a) = h(3)-2
h(2) = h(3)-1 or h(3)-2
h(1) = h(3)+1
h(4) = h(3)-1
h(b) = h(3)-2 or h(3)-3
h(c) = h(3)-2 or h(3)-3
after rotation,
the heights and balances of a, 2, b, and c remain the same. we can deduce the new balances:
the balance of 1 is 0 (if 2 was smaller than 4), i.e. if the balance of 3 was +1, otherwise its +1 (2 was of equal size)
in pseudocode, 1.new.balance = 1 - 3.old.balance
the new height of node 1 is h(2) + 1 = h(3) or h(3) - 1, or h(3) - 1 + 1.new.balance
the leaves/subtrees of node 4 haven't changed, so the balance and height of 4 remain equal
we know the heights of both subtrees of the 3.new, so we can compute the balance:
its either 0 (if 2 was smaller than 4) or -1 (if 2 equals 4 in height)
the height of the entire subtree shrinks when subtree 2 is smaller than subtree 4, i.e. if the old balance of 3 equals +1. In this case you need to recurse upward to adjust weights higher up the tree
summarized the new balances can be computed as follows
4.new.balance = 4.old.balance (i.e. unchanged)
1.new.balance = 1 - 3.old.balance
3.new.balance = -1 + 3.old.balance
recurse = (3.old.balance == +1)
when doing a right-right rotation.
i'll leave the exercise of figuring out the maths for the other three rotations to you.